Decision Trees and Random Forrest Machine Learning Algorithm

 Introduction

Decision trees are a type of model used for both classification and regression. Trees answer sequential questions which send us down a certain route of the tree given the answer. The model behaves with “if this than that” conditions ultimately yielding a specific result. This is easy to see with the image below which maps out whether or not to play golf.

 

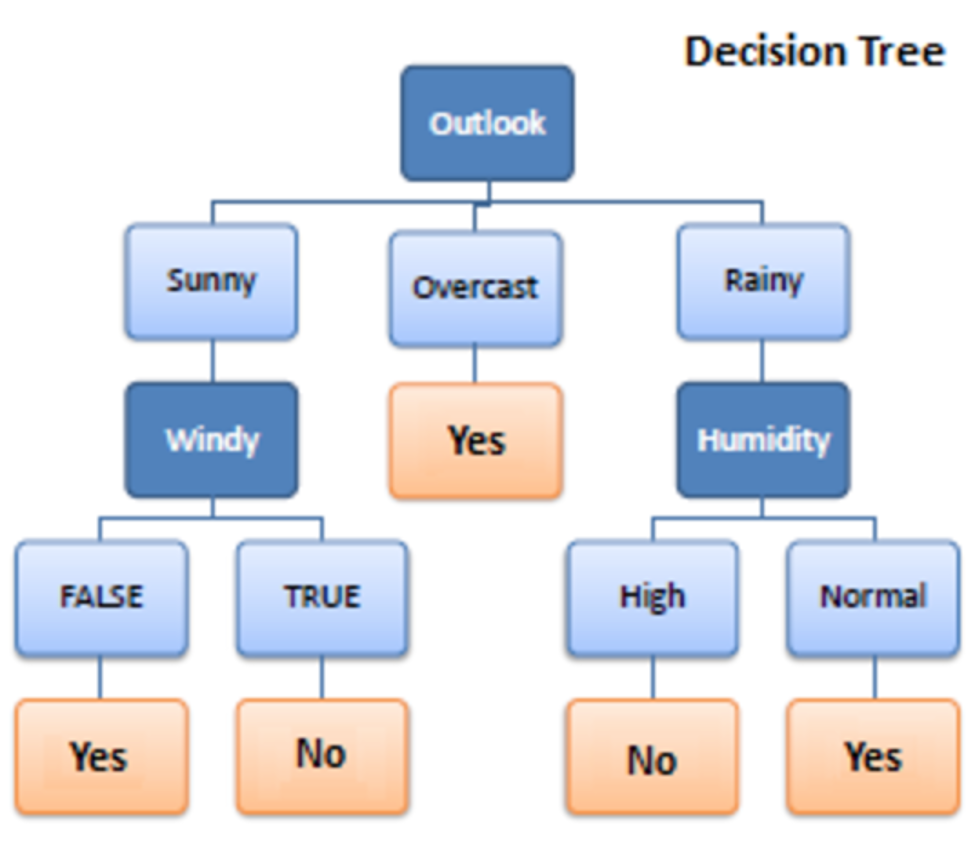
The flow of this tree works downward beginning at the top with the outlook. The outlook has one of three options: sunny, overcast, or rainy. If sunny, we travel down to the next level. Will it be windy? True or false? If true, we choose not to play golf that day. If false we choose to play. If the outlook was changed to overcast, we would end there and decide to play. If the outlook was rainy, we would then look at the humidity. If the humidity was high we would not play, if the humidity is normal we would play.

Tree depth is an important concept. This represents how many questions are asked before we reach our predicted classification. We can see that the deepest the tree gets in the example above is two. The sunny and rainy routes both have a depth of two. The overcast route only has a depth of one, although the overall tree depth is denoted by its longest route. Thus, this tree has a depth of two.

Advantages to using decision trees:

1. Easy to interpret and make for straightforward visualizations.

2. The internal workings are capable of being observed and thus make it possible to reproduce work.

3. Can handle both numerical and categorical data.

4. Perform well on large datasets

5. Are extremely fast

Disadvantages of decision trees:

1. Building decision trees require algorithms capable of determining an optimal choice at each node. One popular algorithm is the Hunt’s algorithm. This is a greedy model, meaning it makes the most optimal decision at each step, but does not take into account the global optimum. What does this mean? At each step the algorithm chooses the best result. However, choosing the best result at a given step does not ensure you will be headed down the route that will lead to the optimal decision when you make it to the final node of the tree, called the leaf node.

2. Decision trees are prone to overfitting, especially when a tree is particularly deep. This is due to the amount of specificity we look at leading to smaller sample of events that meet the previous assumptions. This small sample could lead to unsound conclusions. An example of this could be predicting if the Boston Celtics will beat the Miami Heat in tonight’s basketball game. The first level of the tree could ask if the Celtics are playing home or away. The second level might ask if the Celtics have a higher win percentage than their opponent, in this case the Heat. The third level asks if the Celtic’s leading scorer is playing? The fourth level asks if the Celtic’s second leading scorer is playing. The fifth level asks if the Celtics are traveling back to the east coast from 3 or more consecutive road games on the west coast. While all of these questions may be relevant, there may only be two previous games where the conditions of tonights game were met. Using only two games as the basis for our classification would not be adequate for an informed decision. One way to combat this issue is by setting a max depth. This will limit our risk of overfitting; but as always, this will be at the expense of error due to bias. Thus if we set a max depth of three, we would only ask if the game is home or away, do the Celtics have a higher winning percentage than their opponent, and is their leading scorer playing. This is a simpler model with less variance sample to sample but ultimately will not be a strong predictive model.

Ideally, we would like to minimize both error due to bias and error due to variance. Enter random forests. Random forests mitigate this problem well. A random forest is simply a collection of decision trees whose results are aggregated into one final result. Their ability to limit overfitting without substantially increasing error due to bias is why they are such powerful models.

One way Random Forests reduce variance is by training on different samples of the data. A second way is by using a random subset of features. This means if we have 30 features, random forests will only use a certain number of those features in each model, say five. Unfortunately, we have omitted 25 features that could be useful. But as stated, a random forest is a collection of decision trees. Thus, in each tree we can utilize five random features. If we use many trees in our forest, eventually many or all of our features will have been included. This inclusion of many features will help limit our error due to bias and error due to variance. If features weren’t chosen randomly, base trees in our forest could become highly correlated. This is because a few features could be particularly predictive and thus, the same features would be chosen in many of the base trees. If many of these trees included the same features we would not be combating error due to variance.

With that said, random forests are a strong modeling technique and much more robust than a single decision tree. They aggregate many decision trees to limit overfitting as well as error due to bias and therefore yield useful results.

 

Implementation on the Heart Disease dataset:

We used the same set of train and test split for both random forest and decision tree.  For decision tree we largely left the default parameters.  For the random forest we tweaked the n_estimators with various values ranging from 10 to 300.

Consistently the random forest performed above the decision trees in the setup that we had for our data. With the train test split that we were working with and running the models many times, the decision tree accuracy scores normally ranged from 68% to 75%. For the random forest the accuracy scores ranged consistently from 78% to 82% with a peak around 85%.  We used the random forest to compare with the other algorithms,  givens high accuracy scores.